焊接仿真分析|焊接应力应变场有限元分析
2024-11-28
浏览量:
在焊接时,由于加热的不均匀和热量的流动,导致焊接温度场的分布不均匀,而当构件冷却后,由于温度场分布不均匀,在构件内产生了焊接残余应力和变形。同时由于温度场的不均匀还导致了构件内部组织的相变与蠕变。因此,在进行焊 接残余应力及变形分析之前要先准确模拟其焊接温度场。热弹塑性分析法作为基于有限元分析法成长起来的分析方法,它既考虑了温度场的非线性瞬态热传导问题,还考虑了构件内部材料的力学变化,因此热弹塑性分析理论被广泛应用到焊接过程的残余应力和变形分析模拟计算中。由于对焊接应力场进行有限元分析时,存在材料和几何的非线性问题,计算较为复杂。所以往往将其简化为材料的非线性问题,合理简化了有限元计算。同时,为提升计算精度,使用热弹塑性分析理论,并做出如下几点假设:
- 材料的屈服服从米塞斯(Von Mises)屈服准则;
- 材料在塑性区内的力学行为服从强化准则及塑性流动准则;
- 将微小时间内与温度相关的力学性能和应力应变增量视为线性改变。
对于焊接应力应变场的有限元计算,将米塞斯(Von Mises)屈服准则作为其通用屈服准则,以此来判断材料的屈服状态。等效应力表达式为:
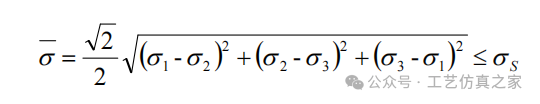
式中,s1、s 2、s 3 为三个正交方向上的主应力,s 为材料的等效应力;s s 是材料单 轴拉伸屈服极限。如想了解更多请扫码关注我们或者拨打一下电话:18086104946当材料处于屈服状态时,其应变是热应变增量{de}p 和弹性应变增量{de }e 之和。同时得到其等效应变公式如下:
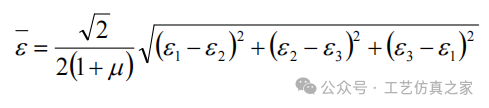
式中,e 1、e 2、e 3为三个正交方向的主应变,m 是材料泊松比。屈服准则又称屈服条件或塑性条件,是判断材料由弹性状态转变为塑性状态的 判据,如上公式表示米塞斯屈服准则和此基础上的等效应变公式,其用在后续焊接仿真分析中,表示焊接构件的状态变化,并能够计算出构件局部的焊接变形。当材料处于塑性状态时,伴随加载继续变大,材料会产生塑性流动。这就是所谓的流动准则,其塑性应力和应变的关系式为:
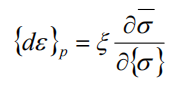
式中,x 为塑性因子,¶ /¶{s}是数量函数 对向量函数{s} 的偏导数。当材料处于塑性状态时,弹性本构关系将不再适用,流动准则则建立了塑性状态下的应力和应变本构关系,用于求解塑性状态下的应变增量,其用在后续焊接仿真分析中,用于计算构件焊接融化后的变形量大小。强化准则是用于描述初始屈服准则由于塑性应变的扩大而变化的过程。因为当材料处于屈服阶段时,会产生塑性流动,塑性应变变大,初始屈服准则发生相应变化。当材料初始屈服准则发生变化时,材料的屈服强度也会发生相应变化,构件材料性能会发生相应变化,因此,学者们往往会对这一变化过程进行相应研究,如下图所示是当前广泛应用的两种强化准则模型。等向强化模型如图 2-3(a)所示,它假定材料的扩张是均匀的且拉压相等的,即其在各个方向上都是平衡的。这是因为焊接过程中,构件的材料和受热是存在变化的,所以要通过假定来降低计算量,减小变化。随动强化模型如图 2-3(b)所示,它指的是材料屈服面只做位移变化不做大小变化,并且当某个方向的屈服应力变化时,其相反方向会发生相反变化。
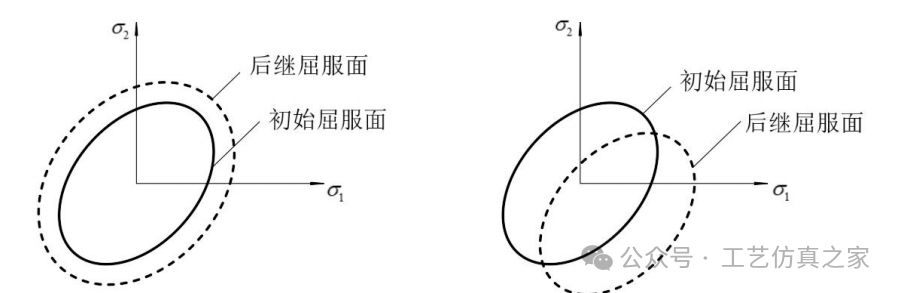
强化模型屈服面示意图(a)等向强化模型;(b)随动强化模型
 鄂ICP备10204367号
鄂ICP备10204367号